Check mathematical equivalence between two latex expressions using TypeScript & mathjs
The Math-validation project aims to determine if two mathematical expressions are equal, either having the same form or not.
There are two main validation types in math-engine: literal validation, which is at its most basic form very similar to a string validation and symbolic validation, which includes the ones from literal, and much more math relevant abilities.
Literal validation
Literal Validation is at its most basic a tuned version of a string validation
By default:
- ignores spaces and parentheses as long as they do not change the meaning of operations: “a+7 +b” will validate against “ ((a) + (7))+b ”
- ignores leading zeros: “0.1” will validate against “.1”
- accepts commas for decimal marks: “1,000” will be equivalent with 1000
Literal Validation offers two configuration options that can be used to validate some variety of forms for an expression:
- Ignore trailing zeros option; allows the evaluation to accept zeros to the right of the decimal place “4.5” will validate against “4.50000000000000”
- Ignore order option; makes validation indifferent to the variables order, as long as it does not change operations meaning. In this case “a+7 +b*c” will validate against “7 + a+bc”, but not against “ac+7+b” ; without it “a+7 +b” will not validate against “7 + a+b”
Symbolic validation
The second type of validation, and the most relevant in mathematics, is symbolic validation. Symbolic Validation attempts to decide if expressions are mathematically equivalent or not. As mentioned before, by default, it offers all configurations presented for literal validation, exceeding it by quite a lot. More on that later, through the implementation example.
In order to check equivalence between 2 expressions, we have to reduce both expressions to the simplest one. Then distribute all coefficients, combine any like terms on each side of the expression, and arrange them in the same order.
Implementation
Next, we will take a look at an example, as part of an implementation, using 2 latex expressions and Symbolic as validation mode. LaTeX is a language used to represent mathematical, and other specialized notations, in type form.
Consider the following expressions:
let firstExpression = "4\\frac{1}{2} + b + ca"
let secondExpression = "\\frac{10}{2} + ac + b- 0.5"
Step 1: Create mathjs instance
We need to instantiate a mathjs object, in this case, specifying fraction as type, for numeric outputs. Fraction allows storing values in terms of a numerator and denominator.
import { all, create } from "mathjs";
export const mathjs = create(all, { number: "Fraction" });(For more details on how to set up and configure mathjs, checkout the official documentation: https://mathjs.org/docs/getting_started.html
Step 2: Input conversion
Mathjs contains a parse function that transforms an expression into an expression tree (also called math-node). Given the fact that the library offers a limited number of operators and does not recognise different notations for the same operators, we created our own parser. Our tokenizer will go through each character of the latex array and build tokens based on the value it finds.
A latex comparison is made at the beggining. If it fails we go forward.
Convert from latex to abstract syntax tree (AST)
The AST is constructed using the shunting-yard algorithm. We use a part of the math-expression library as the skeleton for our tokenizer function. Then we extended and modified it in order to provide the tools we need. Our tokenizer will go through each character or group of characters of the string array and build tokens based on the given rules.
public convert(input, pars?: any) {
this.lexer.set_input(input);
this.advance();
var result = this.statement_list(pars);
if (this.token.token_type !== "EOF") {
throw new ParseError(
"Invalid location of '" + this.token.original_text + "'",
this.lexer.location
);
}
return flatten(result);
}advance(params?: any) {
this.token = this.lexer.advance(params);
...
}// search through each token rule in order, finding first match
result = null;
for (var rule of this.rules) {
result = rule[0].exec(this.input);
if (result) {
let n_characters = result[0].length;
this.input = this.input.slice(n_characters);
this.location += n_characters;
break;
}
}Some of the rules implemented are shown below:
export const latex_rules = [
[measurmentUnit, "UNIT"],
["\\$", "TEXT"],
["\\\\" + "\\$", "TEXT"],
["\\\\text{[a-zA-Z0-9\\s\\\\,\\\\.]+?}", "TEXT"],
["[0-9]+\\s*\\\\frac(?![a-zA-Z])", "MIXED_NUMBER"],
[numberWithCommasAsThousandsSeparator + sci_notat_exp_regex, "NUMBER"],
["[0-9]+(\\.[0-9]*)?" + sci_notat_exp_regex, "NUMBER"],
["\\.[0-9]+" + sci_notat_exp_regex, "NUMBER"],
[",", ","],
["\\*", "*"],
["\\×", "*"],
["\\•", "*"],
["\\·", "*"],
["\\/", "/"],
["\\÷", "/"],
["%", "PERCENT"],
["\\\\%", "PERCENT"],
["−", "-"],
["-", "-"],
["\\+", "+"],
["\\^", "^"],
["\\(", "("],
["\\\\left\\s*\\(", "("],
["\\\\bigl\\s*\\(", "("],
["\\\\Bigl\\s*\\(", "("],
["\\\\biggl\\s*\\(", "("],
["\\\\Biggl\\s*\\(", "("],
["\\)", ")"],
["\\\\right\\s*\\)", ")"],
["\\\\bigr\\s*\\)", ")"],
["\\\\Bigr\\s*\\)", ")"],
["\\\\biggr\\s*\\)", ")"],
["\\\\Biggr\\s*\\)", ")"],
["\\[", "["],
["\\\\left\\s*\\[", "["],
["\\\\bigl\\s*\\[", "["],(The complete list of our simplify rules and the parser can be found here: https://github.com/pie-framework/math-validation/blob/master/src/conversion/latex-to-ast.ts) After the conversion, our expressions will have the following form:
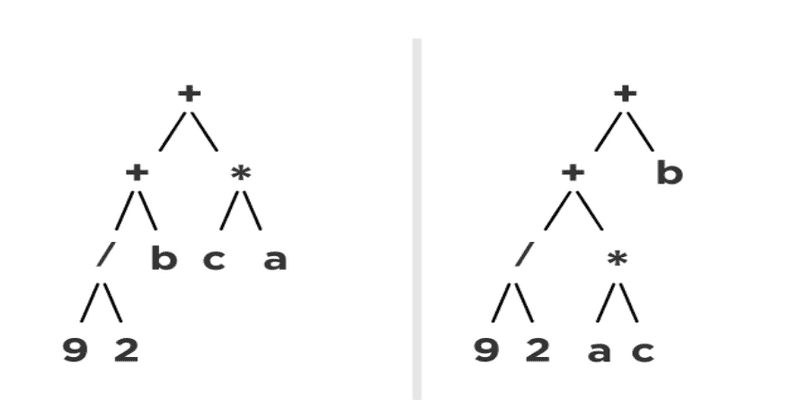
firstExpressionConvertedToAst =
[ '+', 4, [ '/', 1, 2 ], 'b', [ '*', 'c', 'a' ] ]
secondExpressionConvertedToAst =
[ '+', [ '/', 10, 2 ], [ '*', 'a', 'c' ], 'b', [ '-', 0.5 ] ]Input validation
A cutoff is applied to AST in order to avoid running the parser for unvalid input.
Convert from AST to math node
At this point, the AST is converted into a math-node using mathjs. Tokens are converted into operators, functions, relations or units.
After parsing the expressions we get a tree of nodes that can be traversed and the parameters can be ordered where needed.
|
|
Nodes converted to tex, look like this:
firstAstConvertedToMathNode.toTex()=4+\frac{1}{2}+\mathrm{b}+ c\cdot a
secondAstConvertedToMathNode.toTex()=\frac{10}{2}+ a\cdot c+\mathrm{b}+-\frac{1}{2}
Step 3: Rationalization
Try to rationalize math-nodes. And I say try because not all expressions can be rationalized. For example:
mathjs.rationalize("cos(x)+y")
// Error: there is an unsolved function callRationalization is the process of transforming an expression into a rational fraction. Expressions that cannot pass through this process will remain unchanged.
Next, let’s see how the expressions are presented in AST form after rationalization, in order to be easier to follow:
firstExpression=["+", ["+", 4.5, "b" ],["*","c", "a"] ]
secondExpression=["+",["+", 4.5, ["*", "a","c"] ],["b"]]
Step 4: Simplify
Mathjs simplify function applies a set of rules to an expression tree. The default list of rules is exposed as simplify.rules at which custom rules can be added.
Our calculus rules:
const SIMPLIFY_RULES = [
{ l: "n1^(1/n2)", r: "nthRoot(n1, n2)" },
{ l: "sqrt(n1)", r: "nthRoot(n1, 2)" },
{ l: "(n^2)/n", r: "n" },
{ l: "n-n", r: "0" },
{ l: "(n^2) + n", r: "n * (n + 1)" },
{ l: "((n^n1) + n)/n", r: "n^(n1-1)+1" },
{ l: "(n^2) + 2n", r: "n * (n + 2)" },
{ l: "(v1-v2)/n", r: "v1/n-v2/n" },
{ l: "(v1-n)/n", r: "v1/n-1" },
{ l: "n/n1-c1", r: "(n-c1*n1)/n1" },
{ l: "i^2", r: "-1" },
{ l: "pi", r: "3.141592653589793" },
// perfect square formula:
{ l: "(n1 + n2) ^ 2", r: "(n1 ^ 2) + 2*n1*n2 + (n2 ^ 2)" },
{ l: "tzn(n1, n2)", r: "n1" },
{ l: "n1/(-n2)", r: "-(n1/n2)" },
{ l: "sin(n*pi)", r: "0" },
…
]After simplification our nodes look like this (in AST):
firstExpression=["+", ["+", ["/", 9, 2], "b" ],["*","c", "a"] ]
secondExpression=["+",["+", ["/", 9, 2], ["*", "a","c"] ],["b"]]If our math-node is an Array Node, then we have to simplify all the items of the node. Also if the expression is an equation, or an inequality, all parts between equality/inequality sign must be rationalized and simplified separately.
Step 5: Check for infinity
This step was created mostly for the calculus of trigonometric functions, where the result was a very very small number, or on the contrary a very big number, especially when the pi number is involved. In order to be consistent with trigonometric relations, we treated every value smaller or equal than -1.497258191621251e6 as negative infinity and every value bigger or equal than 1.497258191621251e6 as positive infinity.
Some expression that needed this chek are tan(pi/2), csc(360°) or sec(270°)
with the equivalent target "Infinity"
Step 6: Flatten nodes
To make sorting easier, we flatten the nodes where expression allows us. This means that we reduce the form of the expression.
- Strip parentheses where they don’t change order of operations (this happens in flatten). This is done using
transform, a mathjs function, which is a recursive version of map. The callback function is called for every node in the tree and returns a replacement for the node or the original one.
while (node.isParenthesisNode && node.content) {
node = node.content;
}
node = node.transform((currentNode, path, parent) => {
if (
currentNode.isParenthesisNode &&
(parent?.op != "*" ||
(parent?.op == "*" && currentNode.content.op != "+"))
) {
while (currentNode.isParenthesisNode) currentNode = currentNode.content;
}
return currentNode;
});- Transform implicit multiplication in explicit multiplication:
3x => 3*x - Group operations: usually, a mathjs-node tree has two arguments, linked by one operator. The arguments can be another node, with the same operator. If it’s mathematically possible, the nodes will be transformed to link more arguments to only one operator. In order to do this we use a traverse function in a transform callback. Why?
Transformfunction will not iterate through a node that has already been transformed. To go deeper through all childs, we needtraversefunction. We can call this function the recursive version offorEach.
let resultNode = node;
resultNode = resultNode.transform((currentNode, path, parent) => {
while (
firstChildOperator(currentNode, currentNode.fn) &&
!currentNode.isArrayNode
) {
const flatten = currentNode;
flatten.traverse((node, path, parent) => {
if (parent?.fn === node.fn) {
const indexToRemove = path.replace(/[^0-9]/g, "");
parent.args.splice(+indexToRemove, 1) || [];
let argstoAdd = parent.args;
node.args.forEach((arg) => {
argstoAdd.push(arg);
});
node = new m.OperatorNode(node.op, node.fn, argstoAdd);
if (node.fn === "multiply" && node["implicit"]) {
node["implicit"] = false;
}
}
return node;
});
}
return currentNode;
});In our example we are going to reduce an addition operation from both expressions:
firstExpression=["+", ["*","c", "a"], ["/", 9, 2], "b"]
secondExpression=["+", ["b"], ["/", 9, 2], ["*", "a","c"] ]]Step 7: Sort tree nodes
At this point, we are looking for node types and recursively sort the arguments. What we want to achieve here is to arrange the node in its simplest form, from left to right, without impacting the mathematical representation.
If node type is Operator Node and operator is smaller or smallerEq the node is mirrored and larger or largerEq operators are used instead. The same rule applies to Relational Nodes:
"a < b < c" will take the form "c > b > a"
Where the operations are not affected, we want to arrange expressions in the following order:
- Flatten Node ( described at Step 6)
- Operations order: +, -, *, /
- Constant Nodes first, sorted in order by value, then Symbol Nodes sorted alphabetically and Function Nodes
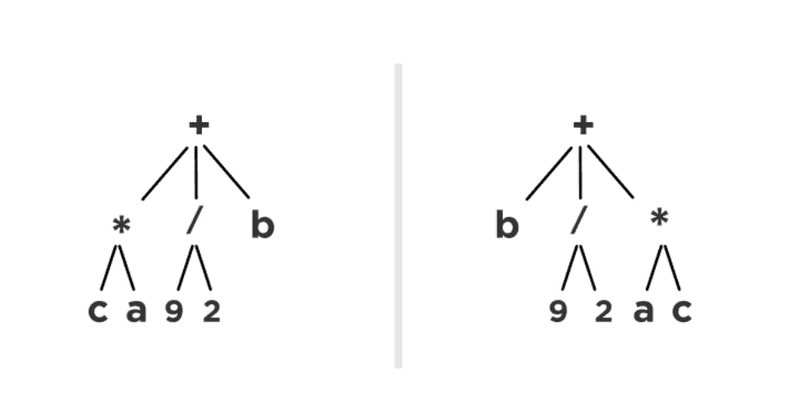
After sorting them, we can see that our expression have the same form and order:
firstExpression=["+", "b", ["*","a", "c"], ["/", 9, 2]]
secondExpression=["+", "b", ["*","a", "c"], ["/", 9, 2]]Mathjs offers various types of nodes : Operator Node, Relational Node, Function Node, Symbolic Node, Constant Node and others. Some simple examples are:
{name: "a"} - Symbol Node
{value: 73} - Constant Node
{op: '+', fn: 'add', args: [Node, Node]} - Operator Node
{conditionals: [ 'smaller', 'smallerEq' ],
params: [
Node { value: [Object] },
Node { implicit: false, op: '*', fn: 'multiply', args: [Array] },
Node { value: [Object] }
]
} - Relational Node(More informations and descriptions about mathjs nodes can be found here: https://mathjs.org/docs/expressions/expression_trees.html)
Step 8: Run node.equals()
Now it is time to determine equivalence of our expressions, by running
sort(firstExpression).equals(sort(secondExpression));
Final words
Throughout this simple example we tackled a few capabilities of math-validation. Some more advanced ones, would be:
- comparing linear equations in one variable
- linear equations in two variables
- 2-way inequalities with one or two unknown variables
- compound inequalities in one variable
- trigonometric identities or functions
- inverse trigonometric functions
- it can also handle degrees, radians and gradians
- recognises similar notation for logarithms and based logarithms
- and others
If this sounds interesting to you, we will show you how this is made in a later lecture.
The complete source code can be found at https://github.com/pie-framework/math-validation and a live demo at https://pie-framework.github.io/math-validation/demo, which can be used with latex expressions.
If something goes wrong when testing expressions, please send us the link containing the input.